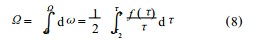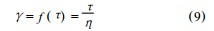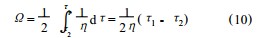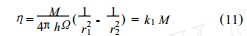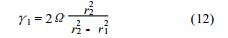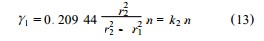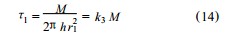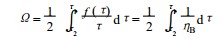粘度计原理介绍:
同轴圆筒旋转黏度计因其测量系统采用圆柱形转筒 ,通过圆筒旋转使被测试样受到剪切而得名. 这种仪器最初产生于 1890 年 ,经过不断完善 ,到上世纪 40 年代后期 ,由于其适用范围广 ,测量结果准确 ,操作方便而得到普遍应用 ,现已成为最常用的流变测量仪器。
这种仪器有两种类型 :一类是内筒以一定的转速旋转 ,用传感器测定作用在外筒或内筒上的转矩 ,简称内旋式或上旋式黏度计. 另一类是使外筒旋转 ,而用传感器测定作用在内筒轴上的转矩 ,称为外旋式或下旋式黏度计[1]. 在旋转速度等条件相同的情况下 ,这个转矩将随流体的黏度而变化 ,黏度越大转矩越大 ,因此测定转矩就可以知道流体的黏度。
1 公式推导
1. 1 旋转黏度计的基本公式
图 1 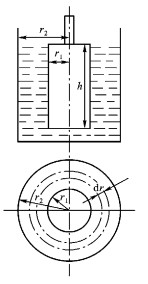
旋转黏度计测量系统示意图
同轴圆筒旋转黏度计测量系统如图 1所示 ,在半径为 r2 的外筒里同轴地安装了半径为 r1 的内筒 ,在两同轴圆筒间充满了黏性流体. 若内筒以等角速度 Ω旋转 ,外筒固定 ,则由于流体具有黏性 ,圆筒旋转时将带动流体运动.
假设流体运动满足以下条件 :1) 两筒为无限长 ;2) 圆筒表面无滑移 ;3) 流体为牛顿流体 ;4) 在垂直于转轴的水平面上 ,流动的流线是圆 ,即速度仅是半径的函数 ,径向和轴向的流动为零 ;5)
运动为稳态的 ,即连续性方程和运动方程的时间导数均为零 ;6) 系统恒温.在内外筒间距旋转轴 r 处取厚度为 d r 的窄环. 考虑到条件 5) ,窄环流体作恒速流动 ,角加速度为零 ,所受合力矩必须为零 ,则窄环内侧和外侧所受的剪切力矩相等. 由于窄环是任意取的 ,故流体内各流层所受剪切力矩相等 ,均等于内筒转动力矩. 各流层剪切力矩为
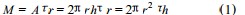
式中 , M 为各流层剪切力矩 , h 为内筒在流体中的高度 ,τ为各流层中的切应力.各流层剪切力矩 M 相等 ,但切应力τ却不相等 ,它是半径 r 的函数. 内筒表面上的切应力

外筒表面上的切应力

这里 r1 < r2 ,故τ1 >τ2.由式(1) 得

将上式对 r 求导 ,整理后得
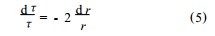
内外筒之间的流体因黏性作用在内筒带动下层旋转 ,各流层质点的角速度不同. 设距旋转轴 r处 ,流体质点的角速度为ω( r) ,线速度 u = rω,则

其中 ω项不引起流体质点的剪切变形 ,又内筒旋转式黏度计 dω/ d r < 0 ,于是切变速度的大小为
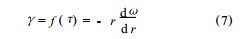
将式(5) 代入式(7) 得到 ,再积分得
,再积分得
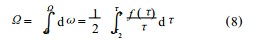
式(8) 便是旋转黏度计的基本公式.
1. 2 牛顿流体的流变测量牛顿流体的本构方程为
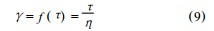
式中 ,γ为切变速率 ,τ为切应力 ,η为流体黏度 ,将其代入基本公式(8) 得
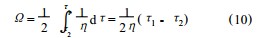
将式(2) 、(3) 代入上式得
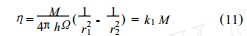
式中 , k1 为仪器常数. 对于指定的测量系统 ,内筒转速一定时 , k1 为常数将τ=ηγ以及式 (11) 代入旋转力矩平衡方程式(1) ,整理得内筒壁切变速率与转速的关系 :
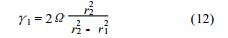
由式(12) 可见 ,牛顿流体的内筒壁切变速率γ1 仅与内筒转速 Ω有关 ,与流体的性质无关. 如内筒的转速为 n ,则
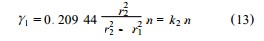
式中 , k2 为由测量系统尺寸决定的系数.由式(2) 得到内筒壁切应力与旋转力矩的关系 :
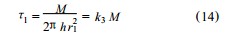
式中 , k3 为转筒尺寸决定的转筒常数.因此 ,对于牛顿流体 ,试验时测量内筒旋转力矩M ,由式 (11) 就可算出被测流体的黏度 ;测量旋转力矩 M 和内筒转速 n ,分别按式 (13) 、(14) 计算切变速率与切应力 ,进而就能绘制流变曲线.
1. 3 非牛顿流体的流变测量和牛顿流体不同 ,对于非牛顿流体 ,其切应力与切变速率是非线性关系 ,其比值τ/γ随切变速率(或切应力) 而变化 ,我们把这种在非牛顿流体场合下求得的不同的黏度值ηi 叫做在切变速率γi 下的表观黏度或非牛顿黏度[2]. 非牛顿流体的流变测量可以采用表观黏度测量方法进行.将非牛顿流体的本构方程γ= f (τ) =τ/ηB 代入旋转黏度计基本公式 ,得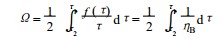
式中 ,ηB 是非牛顿流体的表观黏度.当黏度计测量系统满足窄缝条件 ,也就是内外筒半径远大于两筒间隙时 ,由式 (2) 、(3) 得τ2≈τ1≈τ,即圆筒间各流层切应力相等. 由此 ,ηB 可在上式积分中近似取常值.积分上式 ,采用和牛顿流体相同的步骤得 :ηB = k1 M (15)
γ1 = k2 n (16)
τ1 = k3 M (17)
式中 , k1 、k2 、k3 分别与式(11) 、(13) 、(14) 中意义相同.根据以上分析 ,改变内筒转速 ,同时读取内筒旋转力矩 M 和转速 n ,按式(16) 、(17) 计算 γ1 、τ1 值 ,便可绘制流变曲线[2 ,3]
上述结果是外筒固定 ,内筒旋转的内旋式黏度计测量公式. 若是内筒不动 ,外筒旋转 ,经推导可得到同一形式的关系式 ,只是式中 Ω 为外筒转速. 需要说明的是 ,这种基于窄缝条件的测量方法是一种
设定被测试样各点表观黏度是常量的流体测量的近似方法 ,但由于其测量方法简单 ,且尚能满足一般工程流变测量的精度要求 , 故成为工程界常用的方法.
2 公式修正
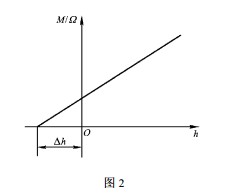
由于仪器构造的限制 ,实际上进行黏度的测定时 ,不可能用无限长的圆筒 ,因此由圆筒的旋转所产生的黏性力矩 ,不仅受两筒侧面部分的影响 ,也受圆筒的上下两个端面部分的影响 ,特别是底面部分的影响更大. 因此有必要对上述计算公式作出修正.当内筒上下端面在被测试样内旋转时 ,两端产生附加力矩 ,相当于增加了内筒的高度 ,则he = h +Δh (18)式中 , he 为修正后的内筒高度 ,Δh 为附加高度.Δh可用试验的方法确定. 在内外筒间充入不同高度的试样 ,以充样高度 h 和单位角速度旋转力矩 M/ Ω作图 ,在 h 轴上的截距就是Δh 值(如图 2)
3 结束语
同轴圆筒旋转黏度计的优点是 ,当内外筒间隙很小时 ,被测流体各部分的切变速度接近均一. 但是由于仪器构造的限制 ,即便操作上正确无误 ,也会使受测试样的实际流动状态和测量的假设条件不完全相符 ,造成一定的测量误差.
单就消除端面效应来讲 ,如果加长圆筒 ,并且将圆筒底面间的距离加大 ,就可以缩小这个影响 ,如圆筒相当长时可忽略这个影响[2]. 某些旋转黏度计为了减小端面附加力矩的影响 ,在构造上进行了改进 ,例如在内筒的上下安装辅助圆筒或者使内筒底部向里凹进 ,使空气进入这里 ,还有把内筒底部做成圆锥等特殊的形状结构. 但是这种结构上的改进仍有局限性 ,测高黏性流体时 ,会因液面波动带来测量数据的不确定。

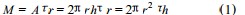



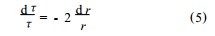

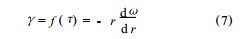
 ,再积分得
,再积分得